Risk

The recent announcement by JP Morgan that they had lost 2 billion dollars through shoddy hedging trades has brought up again the question of how to regulate banks, to prevent them from gambling with public money. Given the important role of banking in the national and world economy, the trust placed in them by the public, and the government's backing of this trust, it seems clear enough to me that banking regulation is important. On the other hand, life is inherently risky. It is not feasible to demand that banks avoid all risk. Banking operations will inevitably involve risk management rather than risk avoidance. What's the difference between risk management and gambling? Surely regulation ought to constrain the sorts of risk taking that is acceptable by banks. But it doesn't appear to be a simple matter, to draw a clear line with only acceptable strategies on one side and only unacceptable strategies on the other.

The mathematical tool that displays most clearly a risk management strategy is a probability distribution. A bank will take the money it holds and invest it in various ways. It can hold currency, or loan the money to customers, or buy treasury bonds, or any number of other ways to try to make money. At the simplest level, a bank should put money into whatever has the best return. If a loan returns 8% while a treasury bond returns only 2%, it surely makes better sense to loan out money rather than buying treasury bonds. On the other hand, it happens all too often that borrowers default. The expected 8% return can turn into a 30% loss. Perhaps the greater safety of treasury bonds outweighs the lesser return. Of course, with enough loans, probably most of them will be paid back and only a few will default.

Somehow a bank needs to estimate with a reasonable degree of accuracy the probabilities of the various possible returns of the various possible investments. One source of risk is simple ignorance, the unknown unknowns. A bank needs to hire the experts who can make accurate estimates, avoid investments where such expertise is unavailable, and keep a watchful eye that the experts don't shy away from too many good new ideas or become overconfident about too many bad old ideas.

Given an understanding of the probabilities of various outcomes from individual investments, and of correlations among those outcomes, a bank can then evaluate proposed portfolios, can derives the probabilities of outcomes for various combinations of investments. Each potential portfolio will imply a cumulative probability distribution with a shape something like:

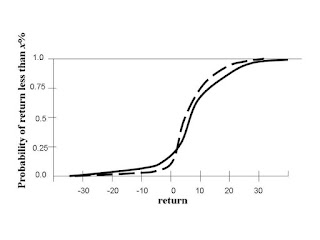
Here the greatest likelihood is that of a moderate return. There is a small probability of a loss, and also a small probability of a very high return. This distribution could represent the existing portfolio of a bank. A small shift in the portfolio, moving money into a new type of investment, will change this distribution somehow.

The most attractive sort of shift is a pure win:

The dashed line shows the new distribution. If at every possible level of return the probability of making less money decreases and the probability of making more money increases, the decision becomes very easy. The proposed new investment is too good to pass up!

Generally, of course, one is faced with more difficult decisions. A typical investment might add some potential for losses, but more likely will bring improved returns:

Another type of investment that often, though not always, make good sense is some kind of insurance. Insurance will reduce the probability of large losses, at the price of smaller returns under other circumstances:

A genuine gamble is one that most likely will lose money but for which there is a smaller probability of a large win:

Of course, real proposals will often involve complex shifts in the probability distribution, giving them aspects of both increasing and reducing risk:

To regulate effectively the risk management practices of financial institutions, one must distinguish between the sorts of risks that can be taken:

• Investments can involve significant unknowable risks, e.g. because of possible political or technological shifts.
• Understanding risks, i.e. accurately estimating the probability of a proposed portfolio, can involve considerable expense that the institution might be unwilling or unable to incur.
• Even when accurate probability distributions are available, it is not clear or simple how to distinguish which distributions represent responsible risk and which constitute violations of the public trust.