Twelves Notes per Octave

Consonant intervals are fundamental building blocks of music. Octaves, perfect fifths and major thirds are the primary consonant intervals in most music. The diagram above shows these intervals for the modern conventional equal tempered tuning with 12 notes per octave. With this kind of diagram, notes separated by an octave are considered equivalent, so, for example, from any C to any G can be considered a perfect fifth.

This diagram makes it clear that conventional tuning is quite dense with consonant intervals. This density implies many enharmonically equivalent relationships, i.e. there are many paths between each pair of notes. This density also tightly constrains the tuning: the interval relationships in this diagram fix the tuning to the standard equal temperament.

I use algorithmic composition to explore the sounds made possible by these networks of interval relationships. Here is a piece built using 12 tone equal temperament.

The main problem with conventional tuning is that the major thirds are rather sharp. Historically, before 12 tone equal temperament became dominant, various forms of meantone tuning were used. The diagram above shows the perfect fifths and major thirds available in meantone tuning. Just one perfect fifth has been removed, but also four major thirds. The resulting freedom allows a range of choice in tuning, trading off accuracy between perfect fifths and major thirds.

Here is a piece in 55edo, a meantone tuning similar to some historial tunings.

Diaschismic tuning is another approach to organizing the network of interval relationships among a set of 12 notes per octave. Now two perfect fifths have been removed from the circle, breaking it into two halves that are connected by perfect fifths. This again allows some freedom of choice in tuning, another way of trading off the errors of perfect fifths and major thirds.

Here is a piece in 34edo, a tuning that supports this network of relationships.

Removing a third perfect fifth allows complete flexibility in tuning perfect fifths and major thirds, in particular allowing just intonation, where a perfect fifth is a 3:2 frequency ratio and a major third is a 5:4 frequency ratio. Removing interval relationships from the network gives more freedom for tuning, but less freedom for composing.

Here is a piece in 118edo, a tuning very close to just intonation.

This graph shows the constraints on tuning for the different interval networks. The x-axis is the size of the perfect fifth, in cents. The y-axis is the size of the major third. The green dot shows just intonation, where the perfect fith and major third are perfectly consonant. The red line shows the tuning possibilities for diaschismic tuning; the blue line shows the possibilities for meantone tuning. I have bracketed the useful regimes for each, where decreasing the error for one interval will increase the error for the other. Outside the useful regimes one can adjust the tuning to reduce the errors for both consonant intervals, which will move one toward the useful regime.

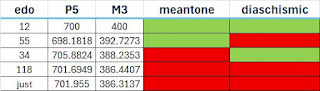
This table gives the tunings, in cents, used in these pieces.