Remapping the Harmonic Table

I am amazed and delighted to discover that Peter Davies came up with a hexagonal keyboard layout very much like mine. He makes keyboards with this layout, as do the folks at C-Thru-Music.

Peter Davies provides this diagram for his keyboard layout:

This layout can be remapped to a kleismatic microtonality in very much the same way that my layout can be.

Note that the pattern of repeated notes in this kleismatic microtonal mapping is not the same as in the conventional mapping. This is where the musical potential for this alternate tuning lies.

Microtonal Remap

One of the challenges of microtonal music is that it is hard to squeeze all the extra notes onto any sort of playable instrument. One approach to solving this problem is to place notes near each other that have a close harmonic relationship. Notes that are very close in pitch might be quite distant harmonically. So an instrument could place far apart notes that are close in pitch. Of course this is easiest with a keyboard, where the mapping of location to pitch is essentially arbitrary. A slide trombone is the other extreme... then again, microtonality is easy on a trombone, if you have a good ear!

Around 1980 I came up with a keyboard layout that could accommodate microtonality, including just intonation. Much more recently I have become interested in alternate key structures on top of microtonal pitch sets. Now I see how to remap my keyboard layout to support the alternate key structure I have been exploring. I would like to share that remapping here.

The keyboard layout covers a flat surface, like a table top. It consists of a hexagonal array of buttons, perhaps something like the chord buttons on an accordion. Of course this keyboard could extend any amount in any direction. A musician needs to be able to reach all the buttons and of course the cost of the instrument will increase with more buttons, but generally a practical instrument will be considerably larger than what I have illustrated here.

I have picked some selected buttons to have a different color, just as an aid for a musician to more easily keep track of location, a bit like the marks often placed on a guitar fretboard. The arrow shows the direction in which pitch increases. The pitches are roughly constant along the line perpendicular to the arrow. I.e. by moving along that line one can explore very small pitch variations.

The notes are laid out on the keyboard by mapping geometric relationships to harmonic relationships. The fundamental harmonic relationship is the octave. Every pair of notes in a the same column with two buttons in between will be an octave apart. An octave is a frequency ratio of 2. To illustrate these frequency ratios, I have picked a button in the middle of the keyboard to serve as a reference frequency and then will show the frequencies of the other buttons as a ration with respect to that reference button. So far all I show is just the two buttons that have octave relationships with the reference button. Of course on a real practical instrument one would generally like to have a much larger series of octaves, so the keyboard would be considerably extended in that octave direction.

The 1980 keyboard layout and the 2013 layout have the same geometrical representation for octaves. They start to split apart from there, though. The next harmonic relationship to consider is the perfect fifth. The 1980 layout uses the perfect fifth as the next building block. Every pair of buttons with the sort of diagonal relationship illustrated will differ in pitch by a perfect fifth. This lets us fill in many more frequency relationships, given that a just perfect fifth is a 3:2 frequency ratio.

The next harmonic relationship is the major third, which is a 5:4 frequency ratio in just tuning. Now things get a little complicated. Three major thirds make a just tuned ratio of 125:64 which is almost but not quite an octave. So the geometrical pattern for the harmonic relationships will be a bit irregular. The columns will follow a pattern of two major thirds, which combine to make a 25:16 ratio, and then a 32:25 ratio to make the complete octave. This completes the mapping of buttons to frequencies: One could use this keyboard layout to play in just tuning, but it can also be used with various temperaments. For example, the conventional 12 pitch equal temperament would look like: Now, instead of frequency ratios, the buttons are labelled with the number of steps up or down from the reference note. In this case the step size is 2^(1/12).

In just tuning every button has a unique pitch and one can find pairs of buttons that differ with arbitrarily fine spacing, limited only by the extent of the keyboard. Temperament limits the number of pitches within any interval. Thus with a tempered pitch set there will be multiple buttons mapped to any given pitch, for example: This geometrical mapping of harmonic relationships can also be mapped to the microtonal 53 pitch equal temperament: Here of course the step size is 2^(1/53). With more finely spaced pitches to choose from, there is less repetition of pitches among the buttons: Up to now this has been a description of the 1980 keyboard layout. In 1980 I had started with just intonation and was exploring various microtonal tempered pitch sets but it was not until the 1990s that I became interested in the 53 pitch equal temperament. Just a couple years ago I became interested in the kleisma, a small interval which is tempered by the 53 pitch set. The kleisma can be considered as primarily constructed from minor thirds. This opens up the intriguing possibility of a keyboard layout based on minor thirds: The 1980 layout had minor thirds for some of these geometric relationships but not for all. There is no way to keep all the minor thirds and all the perfect fifths in a single layout. So the new layout prioritizes the minor thirds and keeps only some of the perfect fifths. Of course musically this is unconventional and probably well nigh perverse, but all the same it might well open up some new and fruitful musical territory. This new layout actually preserves some of the frequencies of the 1980 layout: The mapping to 12 pitch equal temperament is exactly the same as the 1980 layout. The distinction between the layouts is subtle enough that it only appears in a microtonal layout such as the 53 pitch set. The tempering of the kleisma means there is quite a bit of pitch repetition in this layout: Maybe it's time to get out the soldering iron!

Bicycle Tire Pressure

(I have done some more recent work on this: Rotta Model)

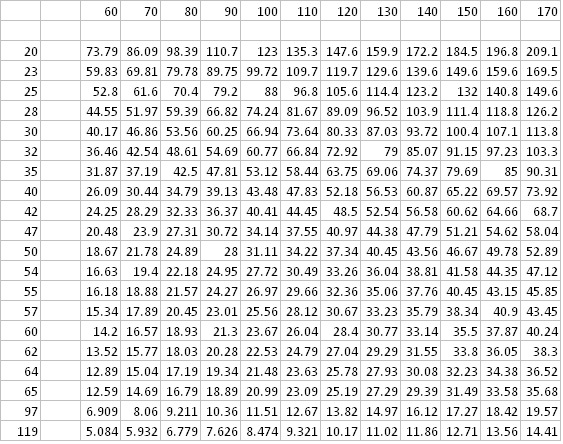
Proper bicycle tire pressure is a topic of endless fascination... and endless debate! On the one hand, what exactly is the goal? It is probably some combination of efficiency, comfort, handling, durability, etc. But the optimum pressure for reaching that goal will depend on many factors: the tire itself - its shape and construction - the load one is carrying, the surfaces on which one is riding, etc.

Frank Berto did some analysis, appearing here and here. Surley makes bikes with very fat tires and has some nice discussion about tire pressure here. There is also a thread on the Thorn forum, where I worked out a hypothesis that, using Berto's "uniform drop" theory, should vary proportionally with the load and inverse proportionally with the 3/2 power of the tire width.

I came up with a constant of proportion to give a reasonable fit with the published graphs by Berto. The fit is not very exact though... whether my formula gives better pressures than Berto's graphs can be left as an exercise for the reader/rider. In any case my formula is easily evaluated for a wider range of loads and tire widths than Berto's graphs cover.

Here, then, is a table of suggested tire pressures. Across the top, find the load, in pounds, on the single wheel, e.g. roughly half the total load on the two wheels of a bicycle. Along the left side, find the width of the tire in mm. The number at the corresponding column and row of the table is then the suggested pressure in psi. Click on the table to get the full image which includes higher loads.